As we mentioned in our previous data structure article, data science is considered one of the most complex fields of studies today.
Currently, most, if not all, of our personal devices are being run on heavily complex data structures and algorithms which would be impossible for us to work out in our heads.
Read More: Understanding Data Structure’s Graph Traversal and Depth First Search
Every day, billions upon trillions of bytes of information are processed in data centers scattered across the globe. As technology soars to greater heights, more and more problems require solutions that only powerful computing systems can accomplish.
To make this possible, computer scientists use graph data structures to represent real-world problems and allow algorithms to solve them.
As promised, in this article, we will discuss how depth first search algorithms, one of the two most important graph traversal algorithms used today.
However, before we jump into the details of the DFS algorithm, let us first understand the difference between a tree and a graph.
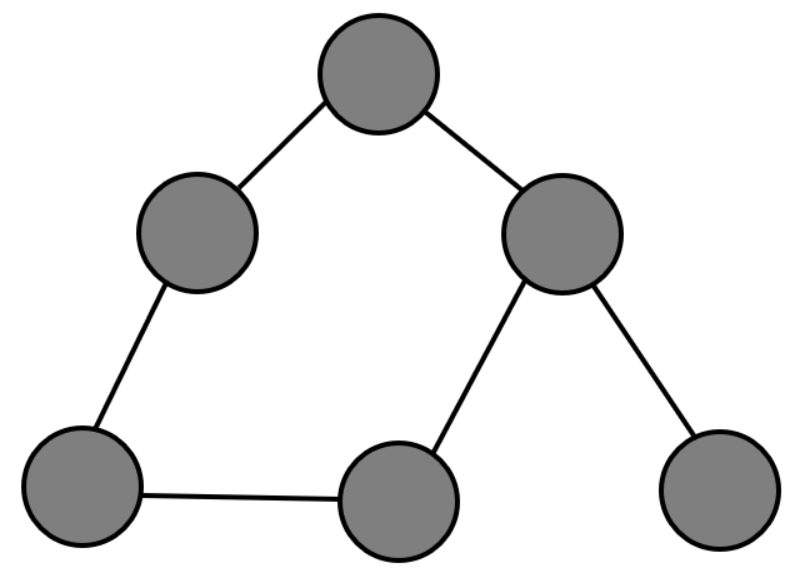
In essence, a tree is considered a special form of a graph. While a graph has more than one path between vertices, a tree only has one path between its vertices.
In a graph, you can start at one vertex and end in another, or you may begin and end at the same vertex. Since there are several paths involved in a graph, there are times that you may find a path that won’t let you traverse the same node or edge twice. Or, you may end up in a path that will enable you to check on a vertex and edge more than once.
This is how a simple data graph may look:
This is a tree:
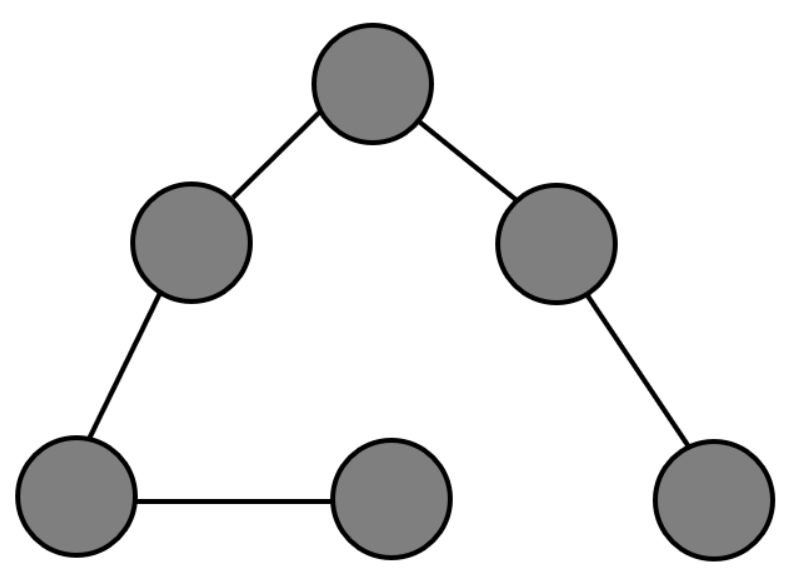
While the two might look similar, they are actually very different from one another.
Tree traversal is often referred to as a tree search. When an algorithm traverses a tree, it checks or updates every vertex in the structure. Then, it marks each node it has visited to ensure that it won’t visit the same node more than once.
Simply put, tree traversal is the process of checking and updating each vertex within a tree once.
Now, aside from visiting each vertex or node, one significant thing to remember when traversing a tree is that order matters.
There are two important techniques when it comes to visiting each vertex in a tree: depth first search and breadth first search.
In a breadth first search, the algorithm traverses the vertices of the tree one level at a time. Meaning, from the parent node, it will visit all children nodes first before moving to the next level where the grandchildren nodes are located. It will go on until the last level has been reached.
For now, that’s all you have to know about the BFS. We will be providing an in-depth discussion about BFS algorithm in our next series.
Understanding Depth First Search
As defined in our first article, depth first search is a tree-based graph traversal algorithm that is used to search a graph. Unlike BFS, a DFS algorithm traverses a tree or graph from the parent vertex down to its children and grandchildren vertices in a single path until it reaches a dead end.
When there are no more vertices to visit in a path, the DFS algorithm will backtrack to a point where it can choose another path to take. It will repeat the process over and over until all vertices have been visited.
Sounds easy, right? Don’t be deceived; there’s nothing simple when it comes to computer science. Even if you already know the basic functions of a depth first search, there are a few other things to consider when traversing a tree.
When checking and updating each vertex, there are three things that a DFS algorithm has to do:
- Read the data stored in the node that’s being checked or updated.
- Check the vertex to the left of the node that’s being checked.
- Check the vertex to the right of the node that’s being checked.
Depth First Search Traversal Strategies
It should also be noted that there are strategies that can be used depending on the order in which the algorithm wants to execute the three tasks mentioned above. These orders are called:
- Preorder
- Inorder
- Post Order
In preorder depth first search, the algorithm will read the stored data starting from the root node, then it will move down to the left node subtree to the right node subtree. This strategy is commonly referred to as DLR.
Root -> Left Subtree -> Right Subtree
In inorder depth first search, the algorithm will visit the left subtree then read the data stored in the root node before moving to the right subtree. This strategy is known as LDR.
Left Subtree -> Root -> Right Subtree
Last but not the least, post order depth first search enables the algorithm to traverse the tree first starting from the left subtree to the right subtree before reading the data stored in the node. This DFS strategy is called LRD.
Left Subtree -> Right Subtree -> Root
To help you better understand the three depth first search strategies, here are some examples.
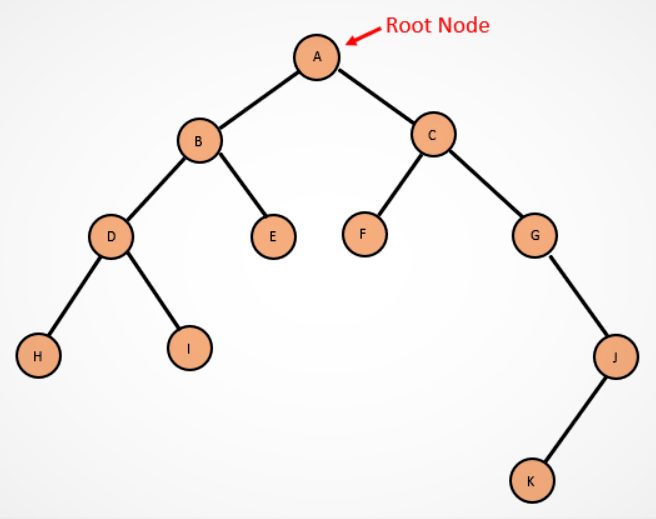
Preorder DFS Strategy (DLR)
As you can see, node A serves as the root node. Following the preorder strategy, the DFS algorithm will traverse the nodes in below order:
- Read data in root node A
- Traverse nodes in left subtree in order of B, D, H, E, I
- Traverse nodes in right subtree in order of C, F, G, J, K
Inorder DFS Strategy (LDR)
In this order, the algorithm will visit all the nodes in the left subtree first, before reading the data and finally moving to the right subtree.
- Visit all nodes in the left subtree starting from H to D, I, B, E
- Read data in root node A
- Traverse nodes in right subtree in order of F, C, G, J, K
Post Order DFS Strategy (LRD)
In post order, the depth first search algorithm will traverse the tree in the following order:
- Visit nodes in the left subtree starting with node H, I, D, E
- Traverse nodes in right subtree in order of B, F, K, J, G, C
- Read data in root node A
Recursion in Depth First Search Traversal
Now, after learning the different DFS strategies that we can use to make a tree search, you also need to know how recursion works.
Recursion is the process of calling a method within that same method, allowing an action to be repeated again and again. As you can see, the DFS algorithm strategies all revolve around three things: reading data and checking nodes in the left subtree and right subtree.
At times, slight changes may occur depending on the process order. Overall though, we’re still going to do the same things repeatedly until all vertices in the tree have been visited.
In essence, a tree has three parts, the data, a left reference, and a right reference. With this information, it’s easy to see that we have to repeat the process of reading the three parts of a node for each node in the three.
Without recursion, the DFS algorithm won’t be able to check all the nodes in a tree because no function will allow it to repeat its action. That said, completing the process of checking the root or parent node won’t be possible.
Since we already know that trees and graphs are being used to model real-world problems, understanding depth first search will now enable you to see how easy or hard it would be to solve a graph structure with a simple glance.
Key Points
To summarize everything that we discussed about depth first search, here are some key points that you should remember:
- Tree traversal is a special kind of graph that usually has only one path between any two vertices or nodes.
- Depth first search traversal of a tree includes the processes of reading data and checking the left and right subtree.
- There are three tree traversal strategies in DFS algorithm: Preorder, inorder, and post order.
- Recursion is the process of calling a method within a method so the algorithm can repeat its actions until all vertices or nodes have been checked.
On our next and last article, we will introduce you to depth first search’s sibling, the breadth first search. Stay tuned for more!


















It is v very interesting and powerful article such such that am empowered intellectually!!!